散布図とは?相関の考え方と散布図の作り方について解説
目次


散布図とは
相関の有無を確認する散布図
散布図とは、縦軸と横軸に、量や大きさを取り、データを当てはまる所にプロットをしたグラフのことです。プロットとは、点を描くことを指します。
2つの変数に関係があるかどうか(相関の有無)を、点の散らばりから確認する手法となります。
本ページでは、相関の考え方や散布図の作成方法について解説しています。
取り上げる2つの変数は2種類あり、結果となる変数である特性と、原因となる変数である要因です。
このスライドのグラフの場合、横軸の身長が要因、縦軸の体重が特性となります。
取り上げた要因は、特性にどう影響するか(相関があるか)、視覚的に確認することが出来るのが散布図の特徴です。ただし、2つの特性の因果関係を示すものではないことに注意が必要です。
相関とは
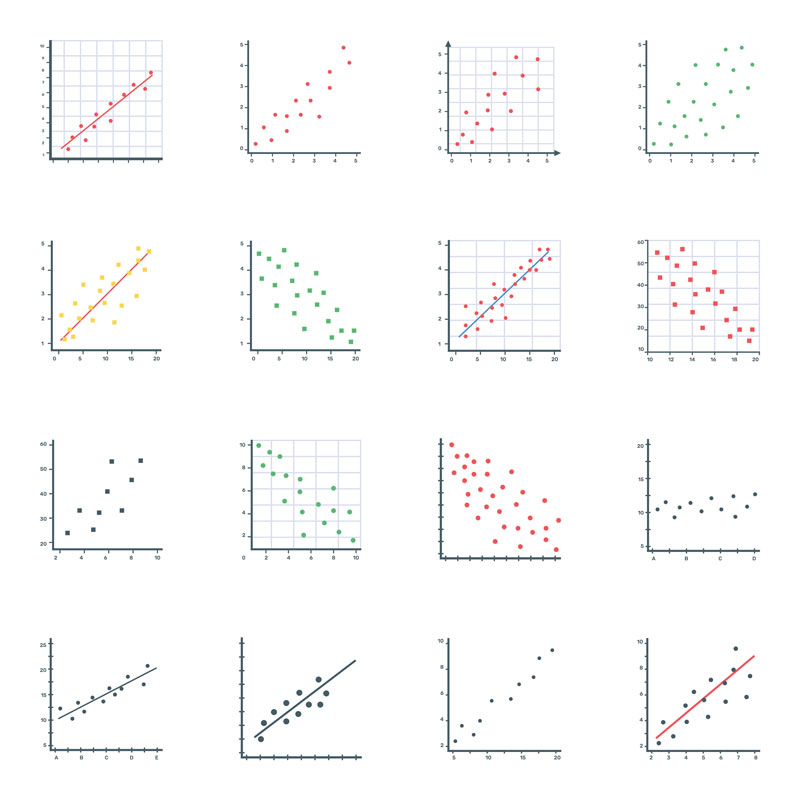
散布図では、次のようなことが確認できます。
1つ目は、正の相関です。
正の相関とは、要因が大きくなればなるほど特性も大きくなるという関係のことを指します。
2つ目は、負の相関です。
負の相関とは、要因が大きくなればなるほど特性も小さくなるという関係のことを指します。
3つ目は、無相関です。
無相関とは、要因が大きくなっても小さくなっても、特性は傾向を示さないというものです。
正の相関、負の相関が出た場合は、その要因を対策していけば、特性(結果)を改善することができます。
一方で、無相関の場合は、いくら要因を対策しても、特性(結果)は変化することがありません。
それぞれの具体例を確認してみましょう。
正の相関の事例
正の相関がありそうな例としては、「身長と体重」「夏の平均気温とエアコンの販売台数」「人口とゴミの量」等が挙げられますね。
負の相関の事例
負の相関がありそうな例としては、「冬の気温とホッカイロの売上」「遊ぶ時間と受験の合格率」等が挙げられますね。
無相関の事例
相関がなさそうな例としては、「身長と学力」「年収と体重」「人口と選挙の投票率」等が挙げられますね。
正の相関、負の相関、無相関、ここに挙げた以外にもたくさんあります。
自分でもいくつか例を挙げて、相関のイメージをしっかりと持っておくようにしましょう。


散布図の作り方
それでは次に、散布図の作り方について確認します。
手順と注意事項
散布図を作る際には、まずはデータを収集します。
相関を見たいもの、例えばあるクラスの身長と体重の関係であれば、身長と体重のデータを収集します。
収集したら、2つのデータが要因と結果であれば、要因をx軸、結果をy軸に設定します。
そして、実際にExcel等の表計算ソフトを使用し、散布図を作成します。
散布図作成においては、縦軸・横軸とも、最大値と最小値を考えた範囲を設定することがポイントです。
あまりに範囲を広くしすぎてしまうと、相関が見にくかったり、判断を間違ってしまうことがあります。
見やすい範囲を設定することを忘れないようにしましょう。
相関係数とは
なお、相関係数についても覚えておきましょう。
相関係数とは、2つの特性の相関関係の強さの度合いを見る統計量のことを指します。
相関係数の計算方法は、ここに示す通りです。
また、散布図においては、Excelの機能として、回帰直線とその数式、R2値も表示させることができます。
回帰直線の数式を用いると、ある要因の値から結果の値の推測が可能です。
R2値は決定係数、回帰直線の数式がどのくらい当てはまっているかを示す指数となります。
散布図の見方と考え方
それでは続いて、散布図の見方と考え方の詳細について確認していきましょう。
散布図の見方の詳細
まず1つ目は、xが増加すればyも増加する、強い正の相関のパターンです。
xが要因でyが結果の場合、xをしっかりと管理すればyを管理することが出来ます。
2つ目は、xが増加すればyも増加傾向を示す、弱い正の相関のパターンです。
yはx以外の要因の影響も受けています。他の要因を調べ、相関のある要因を見つけることが必要です。
3つ目は、xが増加してもyの値に影響が見られないパターンです。
xとyは相関がなく、無相関と言われる状態です。相関のある他の要因を探す必要があります。
4つ目は、xが増加するとyは減少傾向を示す、弱い負の相関のパターンです。
yはx以外の要因の影響も受けています。他の要因を調べ、相関のある要因を見つけることが必要です。
5つ目は、xが増加すればyは減少する、強い負の相関のパターンです。
Xが要因でyが結果の場合、xをしっかりと管理すればyを管理することが出来ます。
散布図を作成した際には、自分の作ったものがどのパターンであるかをしっかりと考えた上で、的確な対応策を考えるようにしましょう。
散布図活用時の注意事項
それでは次に、散布図活用時の注意事項について確認を行います。
因果関係を示すものではない
注意しておかなければいけないこと、それは、散布図は相関を見るためのもので、因果関係を示すものではないことです。
自分が使用したデータの背景をしっかりと考慮した上で、結果の判断を行う必要があります。
どういうことでしょうか?
例えば、この2つの散布図は、それぞれ相関があるでしょうか?
見た目に騙されてはダメ
実はこの散布図、左側の相関がないように見えた方は、3種類のデータが混在しており、それぞれのデータを色分けして見れば相関があります。
また、右側の相関があるように見えた方は、実は相関がないものでした。このように、層別の仕方により、散布図で相関がありそうなのに実はなかったり、相関がなさそうなのに実はあったりするので注意が必要です。
見た目に騙されず、データの背景を押さえる必要があるのです。
もう1つ、次のようなケースはどう考えればよいでしょうか?
ある小学校で、生徒30数名を無作為に選び、算数のテストを受けてもらい、さらにその身長を測定したら身長に対する算数の点数のグラフは右の図のようになりました。
さて、身長と算数の能力は、相関関係があるでしょうか?
実はこのケースの場合、相関はありそうに見えますが、実際にはありません。身長と算数の能力ですので、当たり前と言えば当たり前ですが、このような単純な間違いを起こしてしまうことが少なくないのです。
擬似相関(偽相関)とは
これは、擬似相関、偽相関(にせそうかん)と呼ばれる現象です。
本来2つの変量の間に相関がないのに、取り上げた要因以外の要因が働いて、あたかも相関があるような散布図ができ誤った判断に導かれることを指します。
小学校の場合、年齢と算数の能力に相関があります。また、年齢と身長にも相関があります。
このことが影響し、身長と算数の能力にも見かけ上の相関が現れてしまうのです。
原理原則を考えると、身長と算数の能力に相関がないことは誰でも分かりますので、散布図の見た目だけを見て安易に判断してしまうことは避けなければいけません。
外挿とは
同じような現象として、外挿(がいそう)というものもあります。
外挿とは、散布図をつくった範囲を超えて、その結果を解釈することを指します。
誤った見方となる事も多いので、注意が必要です。
極端な事例ですが、次のようなことです。
年齢と身長の相関を考える際、 5~20歳のデータを取ったら、正の相関が認められました。
このことから、取られたデータの範囲を考慮せず、単に年齢と身長には相関があると決めつけてしまいます。
そして、20~60歳までの範囲でも相関があると結論付けてしまうのです。
身長は永遠に伸びるものではないので、20歳以降では正の相関が当てはまらないのは当然なのです。
特異点の取り扱い
注意点の最後の1つは、特異点(異常値)の扱いについてです。
データの中には、明らかに異常と思われるデータが混在していることがあります。
実務においては、散布図の全体を見て異常値がないか確認をします。
そして、集団から離れた所に点があった場合、その原因を調べます。
調べた結果、異常値の原因が確認できる場合、その点を取り除きます。
異常値の原因が不明の場合は、測定の誤りや作業条件の変更等、特別な原因がないか確認します。
特別な原因がない場合は、その値も含めて判断します。
つまり、特異点が出た場合は、データに測定や記録の間違いがないか確認するようにしてください。
この図の場合、身長170cm、体重46kgは考えにくいため、再測定を行なうかデータの除外を検討します。
特異点を適切に処置しないと、相関係数等の統計量に影響を及ぼすことがあります。
判断をする前に、必ずデータの中身を確認するステップを踏むことが大切です。


散布図まとめ
以上で学んだことをまとめてみましょう。
散布図とは?
- 散布図とは、2つの変数に関係があるかどうか(相関の有無)を、点の散らばりから確認する手法
- 相関の種類には大きく分類すると、正の相関、負の相関、無相関の3つがある
- 散布図を作成する際の注意事項は、「見た目に騙されず、データの中身を吟味すること」「擬似相関、外挿に注意すること」「特異点はデータの背景を含め考える等、取り扱いに注意すること」が挙げられる
いかがでしたか?散布図の作成方法のイメージはつきましたか?
散布図の見た目に騙されることなく、相関を正しく見つけ出して問題解決につなげていきたいですね!
関連学習動画
-
k-014
実務で活用!QC7つ道具の使い方

無料会員限定
2:パレート図とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- パレート図と重点指向
- パレート図の作成方法
- パレート図活用の際の注意点
- パレート図活用とABC分析
- まとめ
-
k-014
実務で活用!QC7つ道具の使い方

公開講座
1:QC7つ道具とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- QC7つ道具とは
- 問題解決のステップとQC7つ道具
- QC7つ道具で必要な層別とは
- 漏れなくダブりの無い層別を
- まとめ
-
k-014
実務で活用!QC7つ道具の使い方

有料サービス限定
7:チェックシートとは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- チェックシートとは
- チェックシートの作り方
- チェックシートの事例
- まとめ
-
k-014
実務で活用!QC7つ道具の使い方

有料サービス限定
8:管理図とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- 管理図とは
- 管理図の見方と考え方
- 管理図の種類
- 管理図の作り方
- まとめ
-
k-014
実務で活用!QC7つ道具の使い方

有料サービス限定
4:グラフとは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- グラフとは
- 代表的なグラフ~円グラフ・棒グラフ・折れ線グラフ~
- 代表的なグラフ~帯グラフ・レーダーチャート~
- まとめ
-
k-014
実務で活用!QC7つ道具の使い方

有料サービス限定
3:特性要因図とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- 特性要因図とは
- ブレーンストーミングの5原則
- 特定要因図の考え方と作成手順
- まとめ

















